Astigmatic Refractive Error: The Power Cross - ppt download

Description

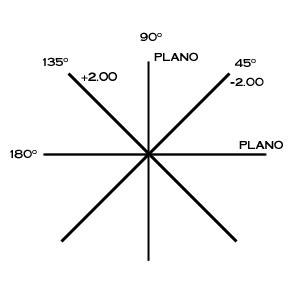
Power Cross The power cross is a concise and convenient format for representing astigmatic error (and its correction) It’s also a source of considerable confusion for ophthalmologists-in-training Trust me when I say that, once you understand it, the Power Cross is your friend!
It’s also a source of considerable confusion for ophthalmologists-in-training. Trust me when I say that, once you understand it, the Power Cross is your friend!
Power is recorded on the meridian of power, which is 90o away from the axis of. power. In this way, a power cross provides an efficient summary of the clinically. relevant refractive properties of the cylinder.
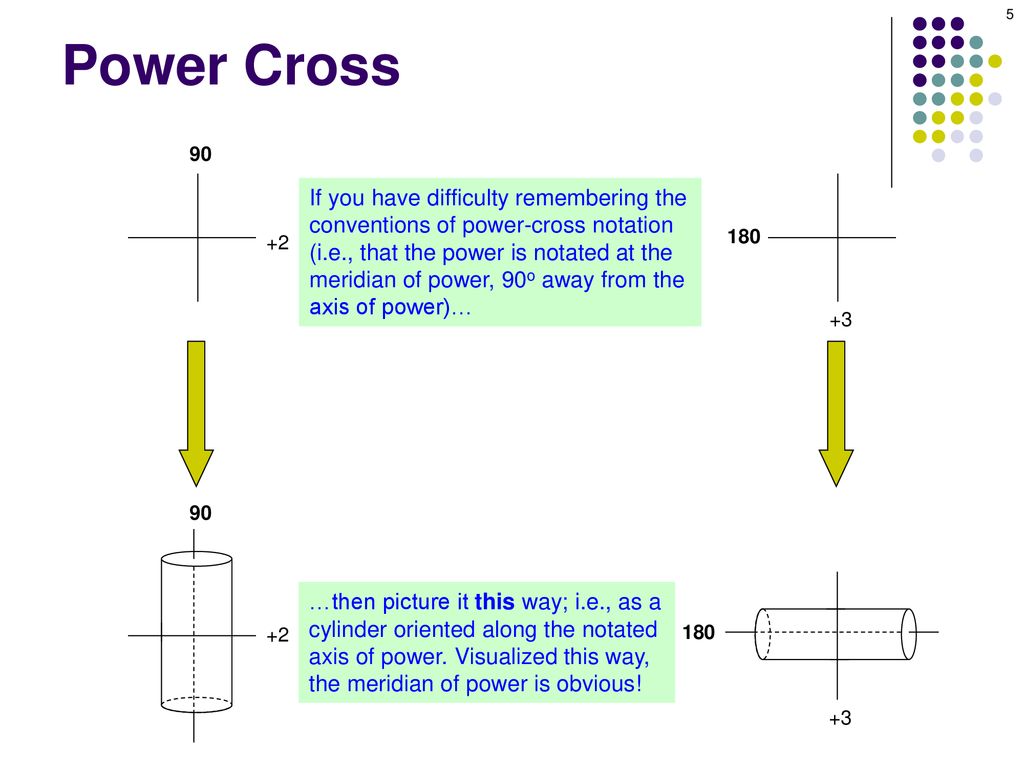
90. If you have difficulty remembering the. conventions of power-cross notation. (i.e., that the power is notated at the. meridian of power, 90o away from the. axis of power)…
90. If you have difficulty remembering the. conventions of power-cross notation. (i.e., that the power is notated at the. meridian of power, 90o away from the. axis of power)… …then picture it this way; i.e., as a. cylinder oriented along the notated. axis of power. Visualized this way, the meridian of power is obvious!
Cylinder combinations can be represented on a single power cross as well. As in the single-cylinder case, the power of each is recorded on its meridian of power, 90o away from its axis.
Cylinder combinations can be represented on a single power cross as well. As in the single-cylinder case, the power of each is recorded on its meridian of power, 90o away from its axis. Say you have a single lens. that is the equivalent of two. cylinders—a +2x090 and. a +3x180.
Cylinder combinations can be represented on a single power cross as well. As in the single-cylinder case, the power of each is recorded on its meridian of power, 90o away from its axis. +2 x 090. The component cylinders. can be written as individual. power crosses… +3 x Say you have a single lens. that is the equivalent of two. cylinders—a +2x090 and. a +3x180.
Cylinder combinations can be represented on a single power cross as well. As in the single-cylinder case, the power of each is recorded on its meridian of power, 90o away from its axis. +2 x 090. The component cylinders. can be written as individual. power crosses… +3 x …and the individual power. crosses can be combined. into a single cross that. represents the lens in its. entirety. Say you have a single lens. that is the equivalent of two. cylinders—a +2x090 and. a +3x180. Power Cross x x
mistake is to treat the power cross like a spectacle/CL prescription. In the present. example, the power cross could be (mis)interpreted as representing the spectacle. correction x 090, or perhaps x 180. Power Cross x x
mistake is to treat the power cross like a spectacle/CL prescription. In the present. example, the power cross could be (mis)interpreted as representing the spectacle. correction x 090, or perhaps x 180. Note that x 090 and x 180 cannot both be correct, as they are not equivalent refractions: x 090 converts to x 180 (not x 180); likewise, x 180 converts to x 090 (not x 090) Power Cross x x
mistake is to treat the power cross like a spectacle/CL prescription. In the present. example, the power cross could be (mis)interpreted as representing the spectacle. correction x 090, or perhaps x 180. What’s the difference between a power cross and a prescription A prescription. is written in spherocylindrical form, whereas a power cross is written in cylinder. form only. If you break down the word ‘spherocylindrical,’ you can see that a. prescription is composed of a sphere power (the first number) and a cylinder power. (the second number, and its axis). In contrast, a power cross simply states the. power and axes of two cylinders—no spherical power is implied. Power Cross x x
with axis 090 has been added.’ (Note that this means the lens has a total of. +5D power at axis 090--the base +3 plus the cylindrical +2.) Here’s where confusion concerning power crosses creeps in. The most common. mistake is to treat the power cross like a spectacle/CL prescription. In the present. example, the power cross could be (mis)interpreted as representing the spectacle. correction x 090, or perhaps x 180. What’s the difference between a power cross and a prescription A prescription. is written in spherocylindrical form, whereas a power cross is written in cylinder. form only. If you break that word down, you can see that a prescription is. composed of a sphere portion (the first power) and a cylinder portion (the second. power, and its axis). In contrast, a power cross simply states the power of two. cylinders—no spherical power is implied. Power Cross x x
with axis 090 has been added.’ (Note that this means the lens has a total of. +5D power at axis 090--the base +3 plus the cylindrical +2.) Here’s where confusion concerning power crosses creeps in. The most common. mistake is to treat the power cross like a spectacle/CL prescription. In the present. example, the power cross could be (mis)interpreted as representing the spectacle. correction x 090, or perhaps x 180. What’s the difference between a power cross and a prescription A prescription. is written in spherocylindrical form, whereas a power cross is written in cylinder. form only. If you break that word down, you can see that a prescription is. composed of a sphere portion (the first power) and a cylinder portion (the second. power, and its axis). In contrast, a power cross simply states the power of two. cylinders—no spherical power is implied. This states ‘the entire lens has a base power of +2, and +3 of cylindrical. power with axis 180 has been added.’ In this version, the lens has a total. of +5D power at axis 180 (the base +2 plus the cylindrical +3). Power Cross x x
with axis 090 has been added.’ (Note that this means the lens has a total of. +5D power at axis 090--the base +3 plus the cylindrical +2.) Here’s where confusion concerning power crosses creeps in. The most common. mistake is to treat the power cross like a spectacle/CL prescription. In the present. example, the power cross could be (mis)interpreted as representing the spectacle. correction x 090, or perhaps x 180. You can see that neither of. these is a proper interpretation. of the power cross below. What’s the difference between a power cross and a prescription A prescription. is written in spherocylindrical form, whereas a power cross is written in cylinder. form only. If you break that word down, you can see that a prescription is. composed of a sphere portion (the first power) and a cylinder portion (the second. power, and its axis). In contrast, a power cross simply states the power of two. cylinders—no spherical power is implied. This states ‘the entire lens has a base power of +2, and +3 of cylindrical. power with axis 180 has been added.’ In this version, the lens has a total. of +5D power at axis 180 (the base +2 plus the cylindrical +3). Power Cross x x
mistake is to treat the power cross like a spectacle/CL prescription. In the present. example, the power cross could be (mis)interpreted as representing the spectacle. correction x 090, or perhaps x 180. What’s the difference between a power cross and a prescription A prescription. is written in spherocylindrical form, whereas a power cross is written in cylinder. form only. If you break that word down, you can see that a prescription is. composed of a sphere portion (the first power) and a cylinder portion (the second. power, and its axis). In contrast, a power cross simply states the power of two. cylinders—no spherical power is implied. In contrast, this is simply stating ‘the lens has a power of +2 at axis 090. and +3 at axis 180.’ Power Cross x x
mistake is to treat the power cross like a spectacle/CL prescription. In the present. example, the power cross could be (mis)interpreted as representing the spectacle. correction x 090, or perhaps x 180. What’s the difference between a power cross and a prescription A prescription. is written in spherocylindrical form, whereas a power cross is written in cylinder. form only. If you break that word down, you can see that a prescription is. composed of a sphere portion (the first power) and a cylinder portion (the second. power, and its axis). In contrast, a power cross simply states the power of two. cylinders—no spherical power is implied. In contrast, this is simply stating ‘the lens has a power of +2 at axis 090. and +3 at axis 180.’ This is true even if the power-cross format is. being used to describe a spherocylindrical lens! Power Cross x x
pick one of the cylinders to serve as the basis for the spherical component, then. adjust the power of the other cylinder as needed. Power Cross x x
pick one of the cylinders to serve as the basis for the spherical component, then. adjust the power of the other cylinder as needed. For instance, in the present. example we could use +2D as our base sphere. The power needed at axis 090. is now in place. What about at 180 Since there is already +2D present there. (courtesy of our +2D base sphere), we need an additional +1 x 180 to produce. the +3D power needed in this axis. Thus, if using a +2D base sphere lens, the. spherocylindrical (prescription) equivalent of our power cross is x 180. Power Cross x x x
pick one of the cylinders to serve as the basis for the spherical component, then. adjust the power of the other cylinder as needed. For instance, in the present. example we could use +2D as our base sphere. The power needed at axis 090. is now in place. What about at 180 Since there is already +2D present there. (courtesy of our +2D base sphere), we need an additional +1 x 180 to produce. the +3D power needed in this axis. Thus, if using a +2D base sphere lens, the. spherocylindrical (prescription) equivalent of our power cross is x 180. Or, we could use the +3D cylinder to create our base sphere. Note that this provides. 1D of plus more than is needed at axis 090. To offset this excess plus we need. -1 x 090 to produce the power needed in this axis. Thus the spherocylindrical. (prescription) equivalent would be x x 090. Power Cross x x x
pick one of the cylinders to serve as the basis for the spherical component, then. adjust the power of the other cylinder as needed. For instance, in the present. example we could use +2D as our base sphere. The power needed at axis 090. is now in place. What about at 180 Since there is already +2D present there. (courtesy of our +2D base sphere), we need an additional +1 x 180 to produce. the +3D power needed in this axis. Thus, if using a +2D base sphere lens, the. spherocylindrical (prescription) equivalent of our power cross is x 180. Note the two prescriptions are equivalent: x 180 converts to x 090, and x 090 converts to x 180. Or, we could use the +3D cylinder to create our base sphere. Note that this provides. 1D of plus more than is needed at axis 090. To offset this excess plus we need. -1 x 090 to produce the power needed in this axis. Thus the spherocylindrical. (prescription) equivalent would be x 090. = x 090. = Power Cross x x x
Let’s take more of a cookbook approach to the conversion of. a power cross to a spherocylindrical correction. Here’s how to. convert a power cross into a spherocylindrical prescription in. four easy steps!
Power Cross 1. Separate the cylinders. Power Cross
(+3) = Make one cylinder the. sphere by adding its power. to the other arm.
(+3) = –(+3) = Make one cylinder the. sphere by adding its power. to the other arm. 3. Subtract the same amount. from the same arm of the. other cylinder.
Combine the two into the. spherocylindrical correction: x (+3) = –(+3) = Make one cylinder the. sphere by adding its power. to the other arm. 3. Subtract the same amount. from the same arm of the. other cylinder.
Eye Error: +1 x x x Sph. We’ve seen this slide before: It was the final result of our. Jackson cross refraction. exercise. Let’s use it as a test. of our new-found power cross. skills by checking the final result. against what would be expected. on the basis of the eye error… (-5) +(-5) Misleading. figure! +4.
Eye Error: +1 x x 090. Check our work… Power cross for correction: -1 x x x Sph. (That is, if this is the power cross of. the eye error, what would the power. cross for the correction be Disregard. vertex distance.) (-5) +(-5) Misleading. figure! +4.
Eye Error: +1 x x 090. Check our work… Power cross for correction: -1 x x x Sph (-5) +(-5)
Eye Error: +1 x x 090. Check our work… Power cross for correction: -1 x x x Sph (-5) To combine the power crosses into a spherocylindrical. equivalent, first add -5 x 180 to the -5 x 090 lens. (This. will make -5 the sphere component of the Rx.)
Eye Error: +1 x x 090. Check our work… Power cross for correction: -1 x x x Sph (-5) = +4. +(-5) To combine the power crosses into a spherocylindrical. equivalent, first add -5 x 180 to the -5 x 090 lens. (This. will make -5 the sphere component of the Rx.) To keep things in balance, subtract that same -5 x 180. from the other power cross, resulting in a power of. +4 x 180 (remember, minus a minus is a plus).
Eye Error: +1 x x 090. Check our work… Cha-Ching! Power cross for correction: -1 x x x Sph (-5) = +4. +(-5) To combine the power crosses into a spherocylindrical. equivalent, first add -5 x 180 to the -5 x 090 lens. (This. will make -5 the sphere component of the Rx.) So the spherocylindrical correction for this eye. error is x 180, which is exactly what. we got with the Jackson cross refraction! To keep things in balance, subtract that same -5 x 180. from the other power cross, resulting in a power of. +4 x 180 (remember, minus a minus is a plus).
Your turn. These are refractive results (not eye errors). Convert each power cross. to spherocylindrical spectacle prescriptions in both plus and minus cylinder formats. Then calculate the S.E. (or can you determine the S.E. simply by looking at the. power crosses )
we will need an extra +1D at axis 090. to get the +2 power needed there. +1. Plus cyl: x 090. Minus cyl: +2.0 –1.0 x 180. S.E.:
Minus cyl: +2.0 –1.0 x 180. S.E.: If we let the base sphere be +2D… we will need a -1D at axis 180 to. get the +1 power needed there.
Plus cyl: x 090. Minus cyl: +2.0 –1.0 x 180. S.E.: Spherical equivalent =
Plus cyl: x 090. Minus cyl: +2.0 –1.0 x 180. S.E.: Spherical equivalent = +2 + (-1)/2 =
Minus cyl: -4.0 –4.0 x 135. S.E.: If we let the base sphere be -8D… we will need an extra +4D at axis 045. to get the -4 power needed there.
Minus cyl: -4.0 –4.0 x 135. S.E.: If we let the base sphere be -4D… we will need an extra +4D at axis 045. to get the -4 power needed there.
Minus cyl: -4.0 –4.0 x 135. S.E.: If we let the base sphere be -4D… we will need an extra -4D at axis 135. to get the -8 power needed there.
Minus cyl: -4.0 –4.0 x 135. S.E.: Spherical equivalent =
Minus cyl: -4.0 –4.0 x 135. S.E.: Spherical equivalent = -8 + (+4)/2 =
Minus cyl: -4.0 –4.0 x 135. S.E.: Spherical equivalent = -4 + (-4)/2 =
we will need an extra +1D at axis 090. to get the +2 power needed there Plus cyl: x 135. Minus cyl: +8.0 –12.0 x 045. S.E.:
we will need an extra +12D at axis 135. to get the +8 power needed there Plus cyl: x 135. Minus cyl: +8.0 –12.0 x 045. S.E.:
Minus cyl: +8.0 –12.0 x 045. S.E.: If we let the base sphere be +8D… we will need an extra -12D at axis 045. to get the -4 power needed there.
Minus cyl: +8.0 –12.0 x 045. S.E.: Spherical equivalent =
Minus cyl: +8.0 –12.0 x 045. S.E.: Spherical equivalent = +8 + (-12)/2 =
S.E.: Plus: x 045. Minus: -4.0 –4.0 x 135. S.E.: Plus: x 135. Minus: +8.0 –12.0 x 045. S.E.: Note that the S.E., being at the ‘dioptric center’ of the conoid of Sturm, is simply the. halfway point between the two cylinder powers. This can be determined by averaging. the cylinder powers—converting to spherocylindrical form first is unnecessary.